PROBABILIDAD

Es muy frecuente para comunicarnos y entendernos.

Se expresa mediante un número entre 0 y 1 (o en porcentajes).

Si no existe la certeza de que ocurran los hechos, existe una esperanza dimensionada y

razonable, de que el hecho anunciado se vea confirmado.

Esta estimación sobre la probabilidad de ocurrencia del evento nos ayuda a tomar decisiones. Por ejemplo: si veo que hay un 15% de padecer infecciones hospitalarias, decido ir o no ir al hospital.

Cuanto más probable es que ocurra un evento, su medida de ocurrencia estará más próximo a 1 o a 100%, y cuanto menos probable, más se aproxima al cero.

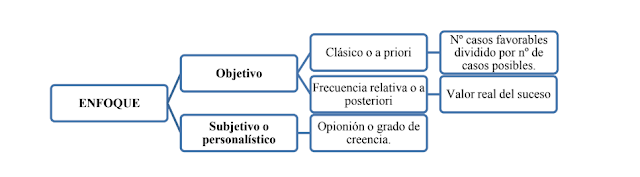
Aunque el concepto es simple, ya que se usa de manera intuitiva, su definición es complicada y tiene tres vertientes:

• Enfoque clásico o a priori: es el número de casos favorables dividido por el número de casos posibles. Es una probabilidad teórica. Por ejemplo: hay cuatro grupos sanguíneos, la probabilidad de que una persona sea del grupo 0, sería del 25%. Luego tenemos la frecuencia relativa o probabilidad a posteriori, que es el valor real del suceso. Por ejemplo: ya depende de factores genéticos, si tus padres son del grupo A tienes más probabilidades de tener ese grupo sanguíneo. Hay fenómenos en los que la probabilidad a priori coincide con a posteriori, por ejemplo, en un dado hay las mismas probabilidades de que salga un número u otro.

PROBABILIDAD SUBJETIVA O PERSONALÍSTICA:

La probabilidad mide la confianza que el individuo tiene sobre la certeza de una proposición determinada.

Por ejemplo: los epidemiólogos se basan en la experiencia para afirmar que el próximo invierno, la epidemia de gripe tendrá una probabilidad del 0,0018 (180 casos por cada 100.000 habitantes).

Este concepto de las probabilidades ha dado lugar al enfoque de análisis de datos estadísticos llamado

“Estadística Bayesiana”.

PROBABILIDAD OBJETIVA:

• PROBABILIDAD CLÁSICA O “A PRIORI”:

Data del siglo XVII (Laplace, Pascal, Fermat), desarrollada para resolver problemas relacionados con los juegos de azar (dados, monedas, ruletas...).

Las probabilidades se calculan con un razonamiento abstracto.

Ejemplo: no hay que lanzar el dado para saber que la probabilidad “a priori” de que salga el 6 es de

1/6=0,16

Definición: Si un evento puede ocurrir de N formas, las cuales se excluyen mutuamente y son igualmente probables, y si m de esos eventos poseen una característica E, la probabilidad de ocurrencia de E es igual am/N

Ejemplo: La probabilidad “a priori” de que salga un As en una baraja de póker (52 cartas) será: