DISTRIBUCIONES NORMALES

• En estadística se llama distribución normal, distribución de Gauss o distribución gaussiana, a una de las distribuciones de probabilidad de variable continua que con más frecuencia aparece en fenómenos reales.
• La gráfica de su función de densidad tiene una forma acampanada y es simétrica respecto de los valores de posición central (media, mediana y moda, que coinciden en estas distribuciones).
• Esta curva se conoce como la campana de Gauss.

ASIMETRÍAS Y CURTOSIS

En la asimétrica hacia la izquierda, aparece primero la meda, luego la mediana y luego la moda (que siempre coincide con el punto más alto ya que es el valor más frecuente) primero viene la media y luego la mediana.

En la asimetría hacia la derecha, aparece primero la mediana y luego la media. En la simétrica coinciden media, mediana y moda.

•  Coeficiente de asimetría de una variable: grado de asimetría de la distribución de sus datos en torno a su media.
• Es adimensional y adopta valores entre -1 y 1.

Los resultados pueden ser los siguientes:

• Si el grado de asimetría es 0 (distribución simétrica; existe la misma concentración de valores a la derecha y a la izquierda de la media). Gráfica de en medio.
• Si el grado de asimetría es >0 (distribución asimétrica positiva; existe mayor concentración de valores a la derecha de la media que a su izquierda). Gráfica de la izquierda. Cuanto más se acerque al 1 más asimétrica es ASIMETRÍA POSITIVA.
• Si el grado de asimetría <0 (distribución asimétrica negativa; existe mayor concentración de valores a la izquierda de la media que a su derecha). Gráfica de la derecha. Cuanto más se acerque al -1 más asimétrica es ASIMETRÍA NEGATIVA.

CURTOSIS O APUNTAMIENTO:

• Coeficiente de apuntamiento o curtosis de una variable, sirve para medir el grado de concentración de los valores que toma en torno a su media.
• Se elige como referencia de una variable con distribución normal, de modo que para ella el coeficiente de curtosis es 0.

Los resultados pueden ser los siguientes:

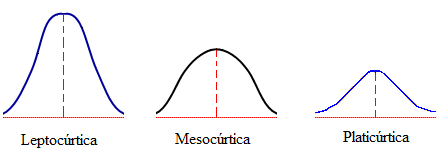
• Si el grado de curtosis es 0 (distribución mesocúrtica). Presenta un grado de concentración medio alrededor de los valores centrales de la variable (el mismo que presenta una distribución normal).
• Si el grado de curtosis es >0 (distribución leptocúrtica). Presenta un elevado grado de concentración alrededor de los valores centrales de la variable.
• Si el grado de curtosis es <0 (distribución platicúrtica). Presenta un reducido grado de concentración alrededor de los valores centrales de la variable. La platicúrtica tiene una mayor medida de dispersión.